Les posteurs les plus actifs de la semaine
| Aucun utilisateur |
Sujets les plus vus
borne sup de la loi exponentielle
2 participants
Page 1 sur 1
 borne sup de la loi exponentielle
borne sup de la loi exponentielle
Bonjour,
Quelqu'un sait comment retrouver la formule des bornes sup et inf de l'intervalle de confiance de la loi exponentielle?
ici j'ai mis la borne sup du taux de défaillance lambda pour n échantillons sur un temps d'essai T et un nombre de défaillance apparu r:
[img][/img]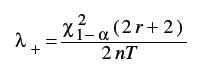
Quelqu'un sait comment retrouver la formule des bornes sup et inf de l'intervalle de confiance de la loi exponentielle?
ici j'ai mis la borne sup du taux de défaillance lambda pour n échantillons sur un temps d'essai T et un nombre de défaillance apparu r:
[img][/img]
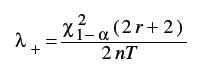
lalmimaj- Nombre de messages : 9
Date d'inscription : 22/11/2012
 Re: borne sup de la loi exponentielle
Re: borne sup de la loi exponentielle
serait ce une colle insurmontable?
lalmimaj- Nombre de messages : 9
Date d'inscription : 22/11/2012
 Re: borne sup de la loi exponentielle
Re: borne sup de la loi exponentielle
Bonjour,
tout dépend de quel intervalle de confiance on parle (c'est comme un estimateur, il en existe beaucoup).
En règle général, On prend un estimateur T de l'espérance mu. On calcule la loi de T, et on prends des quantiles de cette loi. Ensuite le calcul est tjs le même : P(q< T-mu < Q ) = alpha et donc P(mu \in [T-Q,T-q])= alpha
Dans le cas exponentiel, une possibilité serait Estimateur= moyenne empirique, de loi: Gamma(N,theta)/N. Mais il y en a d'autres (EMV...)
tout dépend de quel intervalle de confiance on parle (c'est comme un estimateur, il en existe beaucoup).
En règle général, On prend un estimateur T de l'espérance mu. On calcule la loi de T, et on prends des quantiles de cette loi. Ensuite le calcul est tjs le même : P(q< T-mu < Q ) = alpha et donc P(mu \in [T-Q,T-q])= alpha
Dans le cas exponentiel, une possibilité serait Estimateur= moyenne empirique, de loi: Gamma(N,theta)/N. Mais il y en a d'autres (EMV...)
VV33D- Nombre de messages : 3
Date d'inscription : 04/12/2012
 Sujets similaires
Sujets similaires» Glm diminution exponentielle
» probleme avec loi exponentielle
» Test d'adéquation à une loi exponentielle
» maximum de vraisemblance distribution exponentielle
» Régression exponentielle sous Excel
» probleme avec loi exponentielle
» Test d'adéquation à une loi exponentielle
» maximum de vraisemblance distribution exponentielle
» Régression exponentielle sous Excel
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum