couple de variables aléatoires

Bonjour à tous,

Je suis bloquée face à un exercice que j'ai déjà recommencé 4X sans succès, je n'y arrive pas.

J'aurais besoin de votre aide.

Voici l'énoncé:

Le tableau ci-dessous donne la distribution conjointe de deux variables aléatoires X et Y
X représente le caractère pour, contre ou indifférent de la population belge de plus de 20 ans en ce qui concerne la limitation de vitesse en agglomération
Par contre, Y subdivise cette population en 3 classes d'âge: 20-30 ans, 30-50 ans et plus de 50 ans.


Y 20-30 30-50 50-100
X
pour=0 0.1 0.3 0.1 0.5
contre=1 0.2 0.049 0.05 0.299
indifférent=2 0.15 0.001 0.05 0.201

0.45 0.35 0.2 1




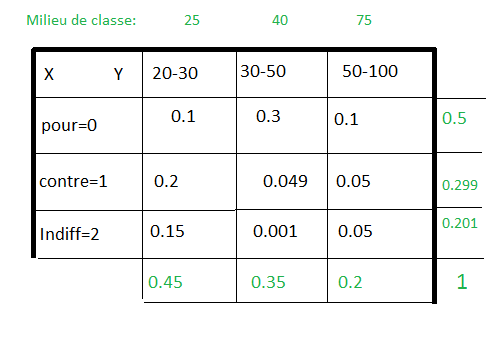
a) Calculez la distribution marginale de X:
J'ai su calculer la distribution marginale pour X et aussi pour Y, donc ça c'est ok.

b) La deuxième question était de savoir si ces v.a étaient indépendantes? la réponse est non
Est-ce que 0.1 est égal à 0.5 X O.45? réponse non deux ces variables sont dépendantes

C'est la dernière question qui me pose problème:

c) Calculez la covariance de X et Y et le coefficient de corrélation. Détaillez votre raisonnement et interprétez votre résultat.

Réponses:
cov(XY) = -2.425 et corr(XY)= -0.167


Dans un exercice semblable, on avait calculé l'espérance de X (moyenne), l'esperance de Y, puis la variance de X et celle de Y

Ensuite pour calculer la correlation on devait d'abord calculer la distribution de XY sous forme de tableau (c'est ici que je suis bloquée)

ensuite grâce à ce tableau on pouvait calculer l'espérance de XY
Puis la covariance de XY et enfin la corrélation de XY

Formules:
cov(XY)= E(XY) - (E(X).E(Y))
corr(XY)= covariance de XY divisée par la racine carrée de la variance de X multiplié par la racine carrée de la variance de Y


Est-ce que quelqu'un sait m'aider??

[b]

bonsoir,
je répond juste à la dernière question pour le calcul de cov(XY).
La distribution de XY est le tableau que tu as donné.
E(XY) = somme des xi yj pij pour i et j variant de 1 à 3. C'est à dire :
E(XY) = 0x25x0.1 + 0x40x0.3 etc...
La somme est assez facile à calculer vu que plusieurs termes sont nuls.
On trouve
E(XY) = 25.79
Pour E(X) et E(Y) on se sert des distributions marginales
E(X)= 0x0.5 + 1x 0.299...= 0.701
E(Y)= 25x0.45 + ... = 40.25
Et avec la formule de la covaraince que tu as donné on trouve bien la réponse.
Pour le coefficient de corrélation utilise ta formule et les distributions marginales pour calculer les écart-types(racine carré de la variance) de X et de Y.
J'espère que cet aide ne vient pas trop tard.
Cordialement

oui un grand merci :-)

j'espere que j'y arriverai aussi bien à mon examen :p