Les posteurs les plus actifs de la semaine
| Aucun utilisateur |
Sujets les plus vus
moments d'une loi normale repliée et tronquée
2 participants
Page 1 sur 1
 moments d'une loi normale repliée et tronquée
moments d'une loi normale repliée et tronquée
Bonjour,
Je suis en train de me casser les dents sur le problème suivant :
Dans des simulations, je tire des valeurs X dans une loi normale centrée (espérance = 0). Jusque là, rien de bien compliqué. Dans cette loi, je m'intéresse en fait plutôt à la valeur absolue de X, et la loi correspondante est une loi normale dite "repliée" ("folded" en anglais), dont l'espérance se calcule facilement. Elle vaut sigma*sqrt(2/pi) (où sigma est l'écart-type de la loi ; voir ici par exemple). Encore une fois, pas trop de problèmes jusque là.
Le problème que j'ai à présent, est que j'ai besoin de tirer des valeurs qui soient supérieures (en valeur absolue) à un certain seuil "a". Je suis donc en fait à la base dans une loi normale tronquée, et ici aussi on peut en calculer l'espérance (voir ici par exemple).
Je pense que vous pouvez à présent entrevoir mon problème : Que vaut l'espérance d'une loi normale centrée d'écart-type sigma, repliée et tronquée au-dessus d'un seuil "a" ?
Impossible de trouver l'information sur le web, et je n'arrive pas à calculer ceci théoriquement.
Si quelqu'un a une idée, elle serait la bienvenue.
Amitiés à tous, Eric.
Je suis en train de me casser les dents sur le problème suivant :
Dans des simulations, je tire des valeurs X dans une loi normale centrée (espérance = 0). Jusque là, rien de bien compliqué. Dans cette loi, je m'intéresse en fait plutôt à la valeur absolue de X, et la loi correspondante est une loi normale dite "repliée" ("folded" en anglais), dont l'espérance se calcule facilement. Elle vaut sigma*sqrt(2/pi) (où sigma est l'écart-type de la loi ; voir ici par exemple). Encore une fois, pas trop de problèmes jusque là.
Le problème que j'ai à présent, est que j'ai besoin de tirer des valeurs qui soient supérieures (en valeur absolue) à un certain seuil "a". Je suis donc en fait à la base dans une loi normale tronquée, et ici aussi on peut en calculer l'espérance (voir ici par exemple).
Je pense que vous pouvez à présent entrevoir mon problème : Que vaut l'espérance d'une loi normale centrée d'écart-type sigma, repliée et tronquée au-dessus d'un seuil "a" ?
Impossible de trouver l'information sur le web, et je n'arrive pas à calculer ceci théoriquement.
Si quelqu'un a une idée, elle serait la bienvenue.
Amitiés à tous, Eric.

Eric Wajnberg- Nombre de messages : 1238
Date d'inscription : 14/09/2012
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
Bonjour,
D'un point de vue analytique je serai bien incapable de te dire, par contre d'un point de vue numérique tu peux essayer ça et peut-être que ça nourrira ta réflexion. Sinon je pense qu'il faut voir auprès d'un vrai mathématicien-stateu :
D'un point de vue analytique je serai bien incapable de te dire, par contre d'un point de vue numérique tu peux essayer ça et peut-être que ça nourrira ta réflexion. Sinon je pense qu'il faut voir auprès d'un vrai mathématicien-stateu :
- Code:
# marche uniquement pour une variable centrée
f <- function(x, s, a) x*dnorm(x, 0, s)/(pnorm(-abs(a), 0, s)*2)*2
integrate(f, 1.5, Inf, s = 1.3, a = 1.5)
# un test avec s = 1.3 et a = 1.5
set.seed(101)
a <- rnorm(1e8, 0, 1.3)
ax <- abs(x)
ax <- ax[ax>1.5]
mean(ax)
droopy- Nombre de messages : 1156
Date d'inscription : 04/09/2009
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
ok, merci. Je vais voir ce que je peux faire avec ça..
Eric.
Eric.

Eric Wajnberg- Nombre de messages : 1238
Date d'inscription : 14/09/2012
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
essaie ça (pour a > 0) :
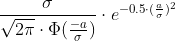
cdlt
- Code:
a <- 1.5
s <- 1.3
integrate(f, 1.5, Inf, s = 1.3, a = 1.5)
s/(sqrt(2*pi)*pnorm(-a/s))*exp(-0.5*(a/s)^2)
cdlt
droopy- Nombre de messages : 1156
Date d'inscription : 04/09/2009
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
Merci,
C'est la piste sur laquelle je planche actuellement. Cependant, plus j'y pense, plus je crois qu'il y a une solution plus simple car, d'une certaine manière, une loi Normale repliée, ça ressemble à une loi Normale tronquée à zéro (les espérances sont évidement les mêmes). Du coup, s'intéresser à calculer l'espérance d'une loi repliée et tronquée en 'a' revient peut-être tout bêtement à s'intéresser à l'espérance d'une loi simplement tronquée en 'a' (a>0), ce qui est simple. Je suis en train de calculer les moments correspondants.
Eric.
C'est la piste sur laquelle je planche actuellement. Cependant, plus j'y pense, plus je crois qu'il y a une solution plus simple car, d'une certaine manière, une loi Normale repliée, ça ressemble à une loi Normale tronquée à zéro (les espérances sont évidement les mêmes). Du coup, s'intéresser à calculer l'espérance d'une loi repliée et tronquée en 'a' revient peut-être tout bêtement à s'intéresser à l'espérance d'une loi simplement tronquée en 'a' (a>0), ce qui est simple. Je suis en train de calculer les moments correspondants.
Eric.

Eric Wajnberg- Nombre de messages : 1238
Date d'inscription : 14/09/2012
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
Bonjour,
en tout cas si tu as la réponse n'hésite pas à nous la donner, je serais curieux de la connaître.
cdlt
en tout cas si tu as la réponse n'hésite pas à nous la donner, je serais curieux de la connaître.
cdlt
droopy- Nombre de messages : 1156
Date d'inscription : 04/09/2009
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
Bon, en fait, c'est donc assez simple. Les moments d'une loi tronquée (notamment une loi Normale) sont bien connus. On trouve plusieurs pages Wikipedia qui expliquent ceci simplement. Il y a même des exemples de code R qui calculent ça (voir par exemple ici).droopy a écrit:Bonjour,
en tout cas si tu as la réponse n'hésite pas à nous la donner, je serais curieux de la connaître.
cdlt
Je viens de recoder ceci en C, et tout marche correctement.
Merci pour ton temps ici droopy pour répondre à ma question.
HTH!
Eric.

Eric Wajnberg- Nombre de messages : 1238
Date d'inscription : 14/09/2012
 Re: moments d'une loi normale repliée et tronquée
Re: moments d'une loi normale repliée et tronquée
Merci pour ce lien.
En tout cas il semble que ma formule soit bonne pour mu = 0 et a > 0 !
cdlt
En tout cas il semble que ma formule soit bonne pour mu = 0 et a > 0 !
cdlt
droopy- Nombre de messages : 1156
Date d'inscription : 04/09/2009
 Sujets similaires
Sujets similaires» Choix entre une distribution Normale et Log-Normale
» fitter une distribution gamma tronquée
» Estimation par Methodes des moments
» Loi de Gumbel: détermination des moments d'ordre k
» distribution normale et log-normale
» fitter une distribution gamma tronquée
» Estimation par Methodes des moments
» Loi de Gumbel: détermination des moments d'ordre k
» distribution normale et log-normale
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
