modèle de mélange de 2 lois Beta

Bonjour

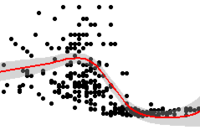
J'ai une distribution d'une liste de données univariées quantitatives (n = 10 000) et l'objectif est de détecter deux groupes (c'est pour un article de bio). La variable est distribuée entre 0 et 1. Très clairement on voit deux "bosses" une très grande à 0.25 et une plus faible vers 0.7 ce qui sous entend qu'il y a bien deux populations.

J'ai donc ajusté un modèle de mélange de 2 loi Beta :
(1-alpha).Beta(a1, b1) +. alpha.Beta(a2,b2)

par un maximum de vraisemblance.

Ainsi j'ai identifié que le paramètre alpha = 0.3.

Ma question est comment attribuer à chaque observation qu'il soit distribué selon la loi Beta 1 ou la 2 ?

Merci beaucoup

Bonne journée

Adrien

Il faut voir comment est écrite la vraisemblance, et peut-être (sûrement) ce problème est discuté dans la littérature.

Dans la mesure où l'estimation des paramètres par ML a également permit d'estimer les paramètres a1, b1, a2 et b2, un moyen de s'en sortir pourrait être de calculer la contribution de chaque observation à la vraisemblance issue de chacune des deux lois correspondantes, séparément, et d'attribuer chaque observation à la loi pour laquelle elle a la vraisemblance la plus élevée.

Mais ceci est juste une proposition personnelle. Je suis sûr qu'il existe d'autres moyens disponibles dans la littérature.

J'espère que cet avis sera utile.

Dans tous les cas, je serais intéressé de savoir s'il existe d'autres méthodes.

Eric.

Merci beaucoup de votre réponse.

Oui le problème n'est pas si évident. Je ne sais pas si vous connaissez le package de R : "Mclust" : qui fait aussi de l'estimation d'un modéle de mélanges puis attribue dans un second temps une classe aux observations.

Cela pourrait être une piste.

Très bonne journée à vous

Adrien

Ok. Merci. Non, je ne connaissais pas Mclust. Je viens d'y jeter un rapide coup d’œil. Il semble que seuls des mélanges de lois Normales sont pris en compte, or vous avez des lois Beta.

Tenez-nous informé si vous aboutissez à quelques chose.

Eric.

Bonjour,

Tu peux utiliser des ratios de densités pondérés par la probabilité d'observer chacune des catégories.
Par exemple avec le mélange de loi normale :

Code:

set.seed(100)
x <- data.frame(x = sort(c(rnorm(100), rnorm(50, 6, 2))))
m1 <- Mclust(x)

## les paramètres estimés :
# les moyennes
means <- m1$parameters$mean
means
          1           2
-0.01036238  5.76534635

# les écarts-types
sds <- sqrt(m1$parameters$variance$sigmasq)
sds
[1] 1.002136 1.599077

# les probabilités (proportion de chaque distribution)
ps <- m1$parameters$pro
ps
[1] 0.6631098 0.3368902

# pour x = 2
predict(m1, newdata = data.frame(x = 2))
$classification
[1] 1

$z
          1         2
x 0.8704123 0.1295877

# densité pour la première loi normale :
d1 <- dnorm(2, means[1], sds[1])
d1
[1] 0.05322405

# densité pour la deuxième loi normale
d2 <- dnorm(2, means[2], sds[2])
d2
[1] 0.01559709

# on les pondère par la probabilité de chacune des deux distributions :
d1 <- d1*ps[1]
d2 <- d2*ps[2]

# on divise par la somme
d1/(d1+d2)
[1] 0.8704123

d2/(d1+d2)
[1] 0.1295877


Tu n'as plus qu'à faire la même chose avec ton mélange de lois béta une fois que tu connais tous les paramètres issus du ML.
On attribue la classe à la distribution qui a la plus forte probabilité. Ici la première.

Cordialement.

[edit]Tu devrais jeter un oeil ici :
https://stats.stackexchange.com/questions/114959/mixture-of-beta-distributions-full-example
[/edit]

re,

Si tu cherches à connaître la proba d'appartenir à la première distribution si x = 1.
En fait ça revient à chercher ceci :

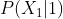
Avec le théorème de Bayes tu tombes sur :

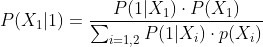
Avec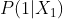 qui la probabilité d'observer 1 avec la distribution qui t'intéresse, avec la loi normale ça donne

Code:

dnorm(1, means[1], sds[1])

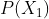et qui est la proportion de ta distribution 1 dans ton mélange (estimée par ton modèle) et
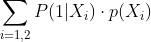est la somme des probabilités obtenues par chaque distribution multipliée par la probabilité de chaque distribution (proportion) ce qui donne en R :

Code:

sum(dnorm(1, means, sds)*ps)

C'est un principe très générique qui va s'appliquer quelque soit le mélange de lois.

Cordialement

Bonjour,

Je n'avais pas vu ta réponse ! Merci beaucoup