Les posteurs les plus actifs de la semaine
| Aucun utilisateur |
Sujets les plus vus
Interprétation Test exact de Fisher / Odds Ratio
2 participants
Page 1 sur 1
 Interprétation Test exact de Fisher / Odds Ratio
Interprétation Test exact de Fisher / Odds Ratio
Bonjour à tous,
Je suis étudiant Kiné, et je suis entrain de réaliser les statistiques de mon mémoire. J'ai réalisé une enquête de pratique.
J'ai déjà eu l'aide d'une statisticienne (qui d'ailleurs collabore au développement de R) qui m'a guidé pour le choix du test.
C'est ainsi que j'ai crée mon tableau de contingence avec mes deux variables qualitatives pour réaliser un Test Exact de Fisher sur R :
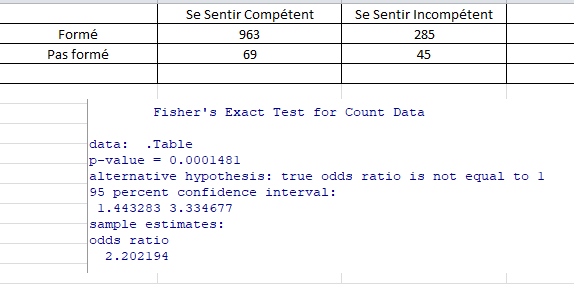
Une fois l'analyse lancé, je trouve un p = 0.0001481
Et un Odds Ratio (OR) de 2.2
Et là je coince pour l'interprétation... J'aimerai vraiment utiliser l'OR pour préciser le lien significatif retrouvé.
J'ai supposé que c’est la formation qui va dire si on est compétent/incompétent (variable dépendante/indépendante à savoir selon réseau bayésien)
: Formation amène la compétence (mon choix)
• Variable indépendante = Formation
• Variable dépendante = Compétence
Donc je compare les modalités de la variable indépendante (formation) = modalité référente sur « R » « pas formé » comparé à « formation/compétent » (car j’ai rentré en premier « formation (+) / compétent »" = ma modalité de base)
Mais je n'arrive pas à décrire ça en "français" pour ma discussion : exemple pour l'instant : Les kinés ont 2,2 chances de plus se sentir « incompétent et d’être non formé » par rapport au fait de sentir « compétent et d’être formé »
Mais cela me semble pas très compréhensible... Comment je pourrai décrire mon ODDS RATIO autrement ? Et l'expliquer aux personnes qui vont lire le mémoire..
Donc voilà si vous avez des astuces, pistes, solutions, je suis preneur !
Merci beaucoup !
Cordialement
Robin.
Je suis étudiant Kiné, et je suis entrain de réaliser les statistiques de mon mémoire. J'ai réalisé une enquête de pratique.
J'ai déjà eu l'aide d'une statisticienne (qui d'ailleurs collabore au développement de R) qui m'a guidé pour le choix du test.
C'est ainsi que j'ai crée mon tableau de contingence avec mes deux variables qualitatives pour réaliser un Test Exact de Fisher sur R :

Une fois l'analyse lancé, je trouve un p = 0.0001481
Et un Odds Ratio (OR) de 2.2
Et là je coince pour l'interprétation... J'aimerai vraiment utiliser l'OR pour préciser le lien significatif retrouvé.
J'ai supposé que c’est la formation qui va dire si on est compétent/incompétent (variable dépendante/indépendante à savoir selon réseau bayésien)
: Formation amène la compétence (mon choix)
• Variable indépendante = Formation
• Variable dépendante = Compétence
Donc je compare les modalités de la variable indépendante (formation) = modalité référente sur « R » « pas formé » comparé à « formation/compétent » (car j’ai rentré en premier « formation (+) / compétent »" = ma modalité de base)
Mais je n'arrive pas à décrire ça en "français" pour ma discussion : exemple pour l'instant : Les kinés ont 2,2 chances de plus se sentir « incompétent et d’être non formé » par rapport au fait de sentir « compétent et d’être formé »
Mais cela me semble pas très compréhensible... Comment je pourrai décrire mon ODDS RATIO autrement ? Et l'expliquer aux personnes qui vont lire le mémoire..
Donc voilà si vous avez des astuces, pistes, solutions, je suis preneur !
Merci beaucoup !
Cordialement
Robin.
Vervaeke Robin- Nombre de messages : 1
Date d'inscription : 31/12/2018
 Re: Interprétation Test exact de Fisher / Odds Ratio
Re: Interprétation Test exact de Fisher / Odds Ratio
Votre question a effectivement plus sa place ici que sur le forum R où vous l'aviez initialement posée.
Le test que vous faites est juste un test pour savoir s'il y ou non une dépendance (on peut parler de corrélation) entre l'entrée de votre tableau compétent/incompétent, et l'autre entrée formé/pas_formé. Le resultat montre que vous pouvez sans problème rejeter l'hypothèse d'indépendance de ces deux entrées. Il y a un lien entre le fait de se sentir compétant, et le fait d'avoir été formé. Par exemple :
La probabilité de se sentir compétant lorsqu'on est formé est de 963/(963+285), soit 77.16 %.
La probabilité de se sentir compétant lorsqu'on n'est pas formé est de 69/(69+45), soit 60.53 %.
Le test que vous fait dit juste que ces deux pourcentages diffèrent. C'est tout.
HTH, Eric.
Le test que vous faites est juste un test pour savoir s'il y ou non une dépendance (on peut parler de corrélation) entre l'entrée de votre tableau compétent/incompétent, et l'autre entrée formé/pas_formé. Le resultat montre que vous pouvez sans problème rejeter l'hypothèse d'indépendance de ces deux entrées. Il y a un lien entre le fait de se sentir compétant, et le fait d'avoir été formé. Par exemple :
La probabilité de se sentir compétant lorsqu'on est formé est de 963/(963+285), soit 77.16 %.
La probabilité de se sentir compétant lorsqu'on n'est pas formé est de 69/(69+45), soit 60.53 %.
Le test que vous fait dit juste que ces deux pourcentages diffèrent. C'est tout.
HTH, Eric.
Dernière édition par Eric Wajnberg le Jeu 3 Jan 2019 - 18:01, édité 2 fois

Eric Wajnberg- Nombre de messages : 1238
Date d'inscription : 14/09/2012
 Sujets similaires
Sujets similaires» Khi2 et interprétation test exact de Fisher
» test exact de fisher/sensibilité regroupement
» Test exact de Fisher
» test exact de fisher
» Khi Deux? ou Test exact de Fisher?
» test exact de fisher/sensibilité regroupement
» Test exact de Fisher
» test exact de fisher
» Khi Deux? ou Test exact de Fisher?
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum