Les posteurs les plus actifs de la semaine
| Aucun utilisateur |
Sujets les plus vus
choix GLM
2 participants
Page 1 sur 1
 choix GLM
choix GLM
Bonsoir à tous,
J'ai un petit soucis en stats :
J'ai des données de comptages de chauve-souris (Tot_chiro) dont voici la distribution ci-dessous :
J'aimerais étudier l'effet de 3 facteurs (Annee, Circuit et Passage) sur la variable réponse Tot_chiro. Ces données étant des données de comptage, j'ai opté pour un Modèle linéaire généralisé de la famille Poisson. Et là c'est le drame, le modèle ne semble pas du tout convenir :
- Les résidus du modèles ne sont pas distribués normalement (cf. QQ-plot)
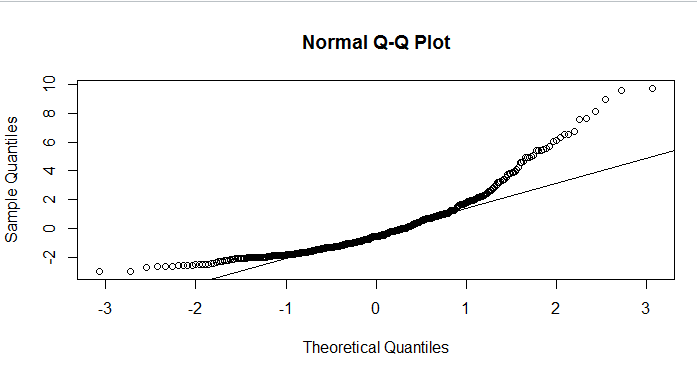
- La sortie R semble indiquer que les variabilité expliquée par mes 3 facteurs est très faible comparée à la variabilité résiduelle

- Confirmation par un graphe Modèle~Tot_chiro
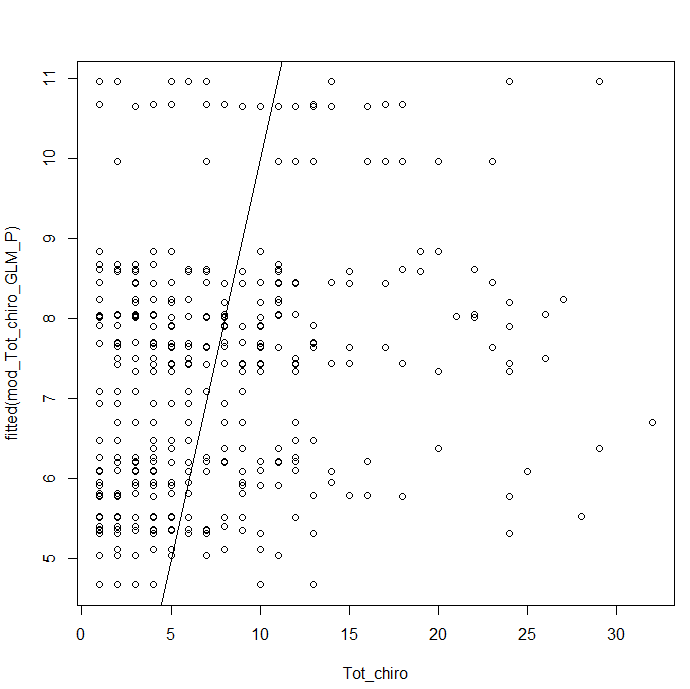
Je suppose que c'est le choix de la famille de Poisson qui fait que mon modèle n'est pas valide mais j'ignore quelle famille ou transformation utiliser pour mes données (binomiale négative ? quasi Poisson ?). Il y a toujours les tests non paramétriques en dernier recours mais si il est possible d'utiliser un modèle c'est quand même mieux ! Avez-vous des idées de modèles / transformations pour mes données ? Merci !
Ci-dessous le script utilisé :
#Modèle linéaire généralisé Poisson (sans interactions)
mod_Tot_chiro_GLM_P <- glm(Tot_chiro ~ (Annee + Passage + Circuit), family = poisson(link=log))
anova(mod_Tot_chiro_GLM_P,test="Chi")
summary(mod_Tot_chiro_GLM_P)
#Qualité du modèle
qqnorm(residuals(mod_Tot_chiro_GLM_P,type='pearson'))
qqline(residuals(mod_Tot_chiro_GLM_P,type='pearson'))
plot(fitted(mod_Tot_chiro_GLM_P)~(Tot_chiro))
abline(0,1)
J'ai un petit soucis en stats :
J'ai des données de comptages de chauve-souris (Tot_chiro) dont voici la distribution ci-dessous :

J'aimerais étudier l'effet de 3 facteurs (Annee, Circuit et Passage) sur la variable réponse Tot_chiro. Ces données étant des données de comptage, j'ai opté pour un Modèle linéaire généralisé de la famille Poisson. Et là c'est le drame, le modèle ne semble pas du tout convenir :
- Les résidus du modèles ne sont pas distribués normalement (cf. QQ-plot)

- La sortie R semble indiquer que les variabilité expliquée par mes 3 facteurs est très faible comparée à la variabilité résiduelle

- Confirmation par un graphe Modèle~Tot_chiro

Je suppose que c'est le choix de la famille de Poisson qui fait que mon modèle n'est pas valide mais j'ignore quelle famille ou transformation utiliser pour mes données (binomiale négative ? quasi Poisson ?). Il y a toujours les tests non paramétriques en dernier recours mais si il est possible d'utiliser un modèle c'est quand même mieux ! Avez-vous des idées de modèles / transformations pour mes données ? Merci !
Ci-dessous le script utilisé :
#Modèle linéaire généralisé Poisson (sans interactions)
mod_Tot_chiro_GLM_P <- glm(Tot_chiro ~ (Annee + Passage + Circuit), family = poisson(link=log))
anova(mod_Tot_chiro_GLM_P,test="Chi")
summary(mod_Tot_chiro_GLM_P)
#Qualité du modèle
qqnorm(residuals(mod_Tot_chiro_GLM_P,type='pearson'))
qqline(residuals(mod_Tot_chiro_GLM_P,type='pearson'))
plot(fitted(mod_Tot_chiro_GLM_P)~(Tot_chiro))
abline(0,1)
Chiro_stats- Nombre de messages : 2
Date d'inscription : 15/06/2016
 Re: choix GLM
Re: choix GLM
Deux choses:
1) Dans une régression log-linéaire (GLM Poisson), les résidus ne sont pas supposés gaussiens, évidement, puisqu'on est dans le cadre de lois de Poisson! Tout va bien donc de ce côté.
2) Le seul réel problème serait que vos données ne suivent pas une loi de Poisson. Un moyen de vérifier ca est de refaire le fit, mais avec "family=quasipoisson" à la place de "family=poisson" et de regarder dans le summary la valeur du coefficient de dispersion (pour l'instant fixé à 1). Si ce coefficient reste proche de 1, alors vos données sont bien décrites par un modèle Poissonnien, et vous êtes dans les clous..
HTH, Eric.
1) Dans une régression log-linéaire (GLM Poisson), les résidus ne sont pas supposés gaussiens, évidement, puisqu'on est dans le cadre de lois de Poisson! Tout va bien donc de ce côté.
2) Le seul réel problème serait que vos données ne suivent pas une loi de Poisson. Un moyen de vérifier ca est de refaire le fit, mais avec "family=quasipoisson" à la place de "family=poisson" et de regarder dans le summary la valeur du coefficient de dispersion (pour l'instant fixé à 1). Si ce coefficient reste proche de 1, alors vos données sont bien décrites par un modèle Poissonnien, et vous êtes dans les clous..
HTH, Eric.

Eric Wajnberg- Nombre de messages : 1237
Date d'inscription : 14/09/2012
 Re: choix GLM
Re: choix GLM
Merci pour ta réponse rapide !
1) Au temps pour moi, les résidus ne sont pas supposés gaussiens mais dans mon script je précise bien que je suis dans le cadre d'une distribution de Poisson, les résidus devraient donc quand même s'approcher de la droite, non ?
2) En tentant avec une quasipoisson, le coefficient de dispersion est estimé à 4,74 ... Avec une binomiale négative ce coefficient tombe à 2,37, avec une déviance résiduelle de 473 (à la place de 1900 en Poisson ...) et les résidus (ainsi que les résultats) semblent plus cohérents (cf. sortie R et graphes ci-dessous). Cela vous semble pertinent d'utiliser ce modèle ? Ou bien la variabilité résiduelle est encore trop importante ?
Avec une binomiale négative :
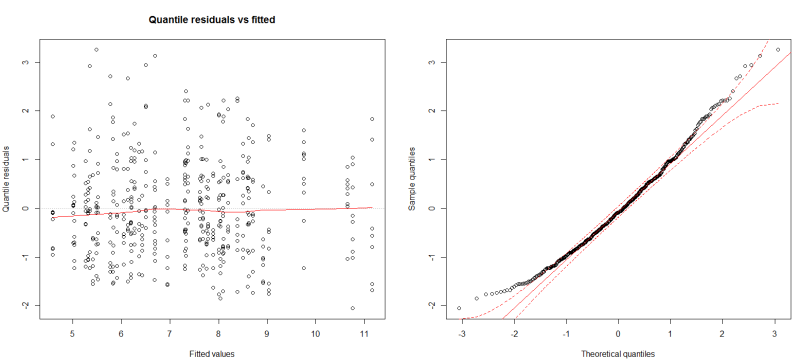
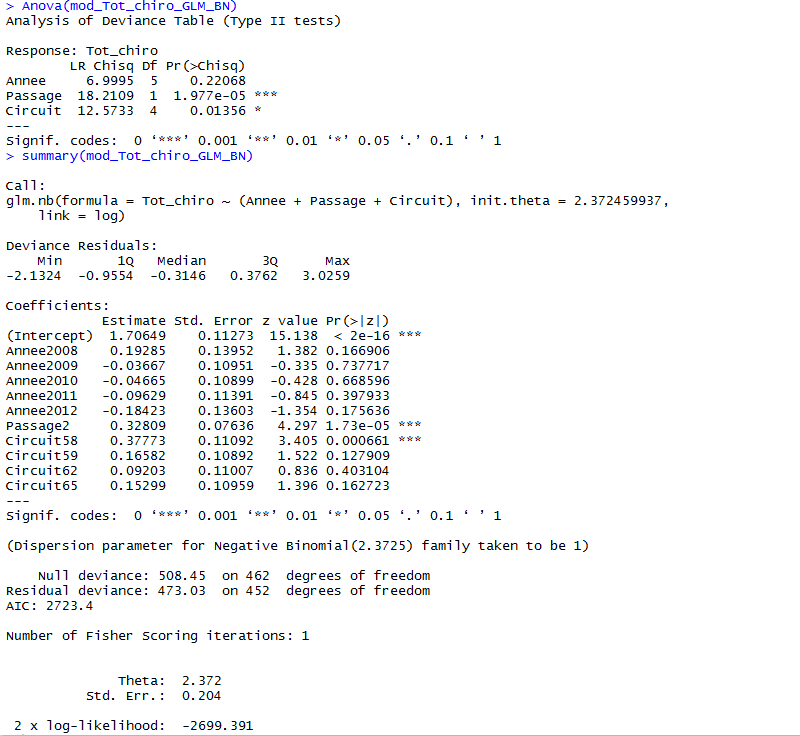
1) Au temps pour moi, les résidus ne sont pas supposés gaussiens mais dans mon script je précise bien que je suis dans le cadre d'une distribution de Poisson, les résidus devraient donc quand même s'approcher de la droite, non ?
2) En tentant avec une quasipoisson, le coefficient de dispersion est estimé à 4,74 ... Avec une binomiale négative ce coefficient tombe à 2,37, avec une déviance résiduelle de 473 (à la place de 1900 en Poisson ...) et les résidus (ainsi que les résultats) semblent plus cohérents (cf. sortie R et graphes ci-dessous). Cela vous semble pertinent d'utiliser ce modèle ? Ou bien la variabilité résiduelle est encore trop importante ?
Avec une binomiale négative :


Chiro_stats- Nombre de messages : 2
Date d'inscription : 15/06/2016
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|
